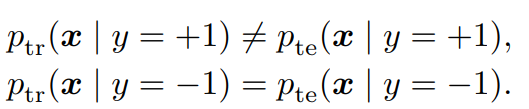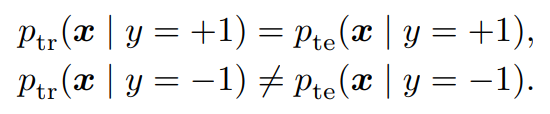https://ojs.aaai.org/index.php/AAAI/article/view/4411
会議はAAAI Conference on AI。
Introduction
Covariance Shiftに対しては、Importance Weightingをサンプルに付与したうえでの、リスク最小化という手法が行われている。これは、密度比pte(x)/ptr(x)である(本来は同時分布であるが、Covariance Shiftではこれと等しい)
この問題設定をPU Learningにも適用した。
Background
問題設定
- データはx∈Rd、Ground Truthのラベルはy∈{−1,+1}である。
- 識別器はg:Rd→Rであり、符号が予測結果で絶対値がConfidenceであった。
- 訓練目標は、Rte(g)=Epte(x,y)[l(yg(x))]の最小化である。
- Samplingの手法はおそらくCase-Control。
- 存在するのはCovariance Shift。以下のようなものである。
ptr(y∣x)=pte(y∣x)ptr(x)=pte(x) - 与えられるデータは、DtrP,DtrU,DteUである。訓練データのDomainではPUが与えられ、テストデータのDomainから得られたデータはすべてUである。
PU Learningについての部分は省略。この論文ではカーネル法を使った線形識別器を使っているので、使ってるPUのリスクの式は以下のようなものである。nnPUではなく、 📄 2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data である。
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data である。
R(g)=πE+[l(g(x))−l(−g(x))]+EX[l(−g(x))] Importance WeightingによるCovariance Shiftの対処
Covariance Shiftに対処するために、密度比w(x)=pte(x)/ptr(x)を用いて、以下のような式の最小化を行う。
Eptr(x,y)[l(yg(x))w(x)] データの重みによって、出現頻度を補正する重みをつけたうえでの最小化ということになる。
これの証明
期待値を積分の形で書き直せることを利用。pte(x)=ptr(x)w(x)であるので、明らかに以下のようになる。(Covariance Shift特有のptr(y∣x)=pte(y∣x)が成り立つことで、同時分布の関係を周辺分布に転用できる)
Eptr(x,y)[l(yg(x))w(x)]=Epte(x,y)[l(yg(x))] 提案手法
R(g)=πE+[w(x){l(g(x))−l(−g(x))}]+EX[w(x)l(−g(x))] 単純に、密度比を乗じることが数学上正しいので、このように使う。理由としては以下のような式変形。
ここで、w(x)の推定はサンプルの周辺分布のみを使っており、ラベルの情報は不要である。
このw(x)は、📄 2021-Survey-A Comprehensive Survey on Transfer Learning (Part1) Instance Weighting Strategy の2012, Sugiyamaの手法で行っている。
2021-Survey-A Comprehensive Survey on Transfer Learning (Part1) Instance Weighting Strategy の2012, Sugiyamaの手法で行っている。
なお、上の式でのEXでの期待値はTrainのDomainから計算しているが、現にTest DomainのUnlabeledDTUからサンプルしたデータはあるので、それについての計算をしてもよい。
見る感じだとこっちのほうがよさそうで計算結果が安定するが、どうやら実験してみた形だとTrain Domainから密度比で変換したほうがいいらしい。
理由としては密度比は完ぺきに推定できていないのでバイアスが生じるが、同じw(x)を乗じていれば同じようなバイアスがかかっている。EXをTest Domainで計算すると片方の項はバイアスがかからなくなり、それで不整合で性能が落ちるのではないか?
Covariance Shiftの効果
Covariance Shiftについては、2種類考えることができる。
- PositiveだけCovariance ShiftしてNegativeはそのまま。
- NegativeだけCovariance ShiftしてPositiveはそのまま。
PositiveだけCovariance ShiftしてNegativeはそのまま
具体的には以下のようになる。
この時、以下が成り立つと嬉しい。って、成り立たないからDomain Shiftがあるわけだろ!
πtrptr(x∣y=+1)=πtepte(x∣y=+1)ptr(x,y=+1)=pte(x,y=+1) これが成り立たないからこそ、w(x)による補正が必要で、これがなければE+の項にバイアスがかかってしまう。
NegativeだけCovariance ShiftしてPositiveはそのまま
具体的には以下のようになる。
この時、w(x)による補正は不要である。
pte(x,y=+1)=πtepte(x∣y=+1)=πteptr(x∣y=+1) 上式が成り立つので、E+の式の書き換えで以下のようにすればいい。
πteEtr+[l(g(x))−l(−g(x))]+EteX[l(−g(x))] 密度比推定しないので、こっちのほうがずっと学習としては安定する。
Class PriorがShiftする場合
ptr(x∣y)=pte(x∣y)ptr(y)=pte(y) PU Learningでは、以下のようにUnlabeledが得られている。
pte(x)=πtepte(x∣y=+1)+pte(x,y=−1) これを使うと、Class PriorがShiftする場合は、以下のようにNegativeだけCovariance Shiftした時と同じ式で学習すればいい。
両者の違いは、p(x∣y=−1)はTrain, Testにおいて同じであるかどうかだけ。Class PriorがShiftする場合はこれは同じである。
πteEtr+[l(g(x))−l(−g(x))]+EteX[l(−g(x))] 実装
識別器はカーネル法のSVMを使っている。
推定する密度比は以下のように、密度比を直接推定する。
低密度の領域では密度比が非常に大きい値か小さい値をとりうるので、それを防いで安定に計算するべくハイパラα∈[0,1]を導入した以下のもので推定する。
wα(x)=(1−α)ptr(x)+αpte(x)pte(x) α=0の時は普通の密度比である。
これを用いて、最小二乗法でフィッティングを行う。
2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data である。
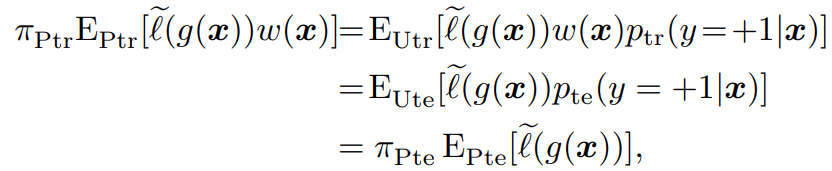
2021-Survey-A Comprehensive Survey on Transfer Learning (Part1) Instance Weighting Strategy の2012, Sugiyamaの手法で行っている。